Вопрос 9: Итерационные методы размещения элементов.

Алгоритм перестановок.

Необходимо некое начальное решение задачи.

1. Выбор элементов, учавствующих в перестановке.
2. Пробная перестановка и расчёт критерия.
3. Выбор лучшего варианта и перестановка.
4. Переход к следующей итерации или остановка.

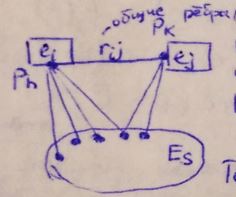
$E_S$ - подмножество элементов, имеющих общие рёбра с $e_i$ или $e_j$

$L_{nach} = \sum_{S} r_{is} d_{hp(s)} + \sum_{S} r_{js} d_{kp(s)} + r_{ij} d_{hk} + L_{ost}$

$r_{ij} d_{hk}$ - длина общих сеодинений

$L_{ost}$ - длина остальных сокдинений

Теперь осуществим парную перестановку $L_{new} = \sum_{S} r_{is} d_{kp(s)} + \sum_{S} r_{js} d_{hp(s)} + r_{ij} d_{hk} + L_{ost}$

$\delta L_{ij} = L_{nach} - L_{new} = \sum_{S} (r_{is} - r_{js})(d_{kp(s)} - d_{hp(s)})$

$\delta L_{ij} > 0$ - удачная перестановка

Выбор кандидатов на перестановку:

1. random - случайный выбор элементов, лучше придумать какой-нибудь критерий выбора.
2. Сначала все вершины графа схемы ранжируются по убыванию локальных степеней (кол. рёбер подходящих к элементу) $\rho(e_1) >= \rho(e_2) >= ...>= \rho(e_n)$ чем больше соединений подходит к элементу, тем важнее найти хорошее положение на МП (для 1-го соединения (элемента) (n-1) вариант, для 2-го (n-2) варианта, для 3-го (n-3), и тд, т.е. факториал всего, для выбранного элемента смотрим только одну перестановку), или по d - суммарной длине соединений, подходящих к элементу $d(e_1) >= d(e_2) >= ...>= d(e_n)$.

Метод соседних перестановок

$\frac{n(n-1)}{2}$ - перестановок

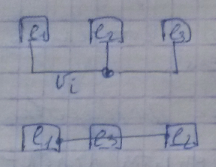
Рассмотрим $M_{e_i} = \sum_{j} r_{ij} - \sum_{\alpha} r_{i\alpha}$, где $e_i : x_j < x_i$, левее $e_i$, $e_{\alpha} : x_{\alpha} >= x_i$ правее. Коэффициент насколько изменяется длина соединений элемента $e_i$, если мы сдвинем его на 1 в одном из направлений.

Изменение длины $\delta L = M_{e_{i\leftarrow}} + M_{e_{\beta\rightarrow}} - 2r_{i\beta}$, где $2r_{i\beta}$ - число общих рёбер у соответствующих элементов $e_i$ и $e_{\beta}$.

Силонаправленный алгоритм релаксации (Алгоритм групповых перестановок)

Можем ли определить положение элемента так, чтобы сумма длин к нему подходящих была минимальной? ДА. 1) Минимизация длины проводников - Центр масс 2) Введение сил притяжения $\Rightarrow$ место, где $F_{ij} + P_{ij} = 0 \Rightarrow$ находим точку, куда поместить A. ТЦ(А) - точка цепи А.

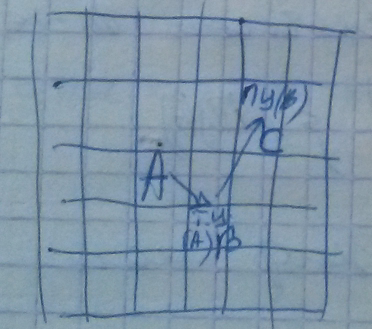
A - первичный элемент/напр., элемент с максимальным числом соединений.

Алгоритм: 1) Выбор элемента А 2) Находим ТЦ(А) 3) Находим ПЦ(А) (Первичная позиция цепи (А), считалась когда все элементы находились в тех местах, которые соответствовали начальному размещению) 4) ТЦ(В) $\Rightarrow$ ПЦ(В) 5) ТЦ(С) $\Rightarrow$ ПЦ(С) и т.д.

Алгоритм попарной релаксации

1) ПЦ(А) первичного элемента 2) Окрестность ПЦ(А) $\rightarrow$ eps(ПЦ(A))

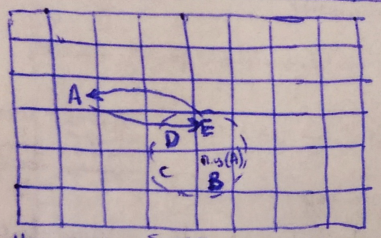
3) ПЦ(В), ПЦ(С), ПЦ(D), ПЦ(Е) 4) Окрестности eps(ПЦ(В), eps(ПЦ(С)), eps(ПЦ(D)), eps(ПЦ(Е)). Каждый элемент должен только приблизиться к ПЦ! Если ПЦ(Е) попала в окрестность А, то меняем их местами. Наилучший обмен с тем элементом, чьё ПЦ ближе всего к позиции первичного элемента. Здесь мы стараемся не просматривать все возможные перестановки.

Алгоритм Гото (объед. двух предыдущ. алг.)

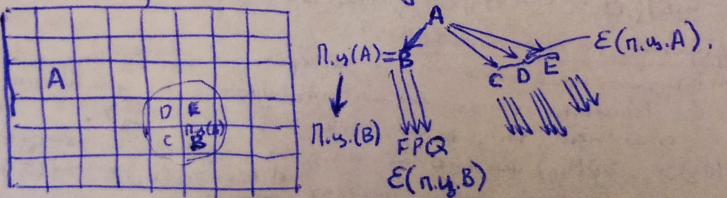Конец, если последний элемент попадает в пустую позицию.

Рекомендации:

• ограничить длины цепочки
• ограничить eps тремя позициями
• отсечение всех возможных ветвей (боковые ветви)