Вопрос 2: Модели схем в задачах автоматизированного конструирования.
Модели являются способами представления графа, который строится по схеме.
Обозначения
E=e1,e2,...,en - множество элементов
U=u1,u2,...,um - множество цепей
Z=⎝⎜⎜⎛z11z21⋮zn1z12z22⋮zn2......⋱...z1n1z2n2⋮znnn⎠⎟⎟⎞ - таблица контактов (выводов) элементов
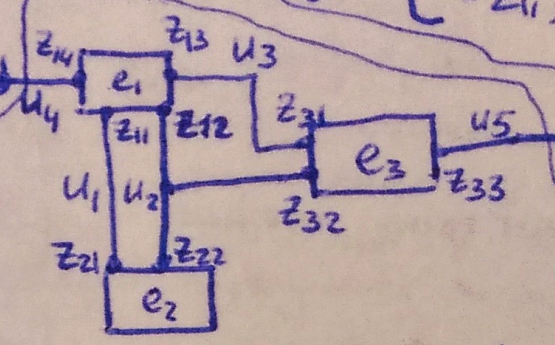
Модель 1: Граф коммутационной схемы (ГКС)
Способ описания 1: матрица A и B
A=e1⋮enz111⋮1......⋮...z1n10⋮0......⋮...zn11⋮1......⋮...znnn1⋮1
B=u1⋮umz111⋮1......⋮...z1n10⋮0......⋮...zn11⋮1......⋮...znnn1⋮1
В столбцах матриц A и B может быть только одна единица.
Способ описания 2: матрица соединений T
T=e1⋮enz111⋮1......⋮...z1n10⋮0......⋮...zn11⋮1......⋮...znnn1⋮1
Элементами матрицы являются номера цепей, которые должны подходить к соответствующему элементу и к соответствующему контакту (Выводу).
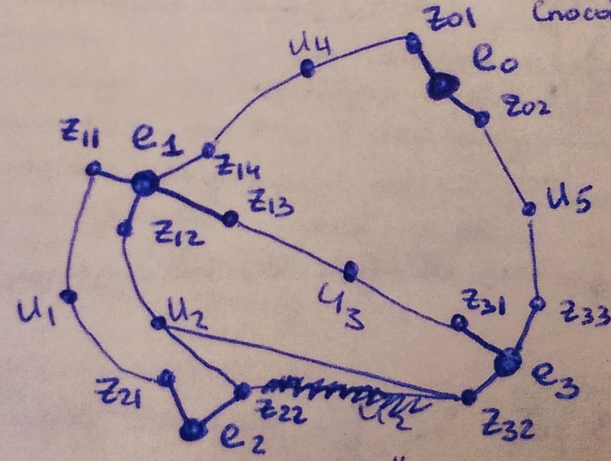
Модель 2: Граф цепей

Q=e1⋮enu11⋮1......⋱...um1⋮0
qi,j=1 если ei принадлежит цепи uj.
Модель 3: Гиперграф
Под ребром понимается множество его вершин:
u1=e1,e5,...;...um=e3,e5,...;
Под вершиной понимается множество его ребер:
e1=u1,u5,...;...en=u3,u5,...;
Модель 4: Взвешенный граф схемы
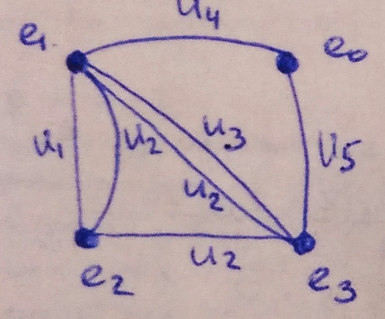
R=e1⋮ene10⋮4......⋱...en2⋮0
Элементы матрицы показывают количество путей из одной вершины в другую.
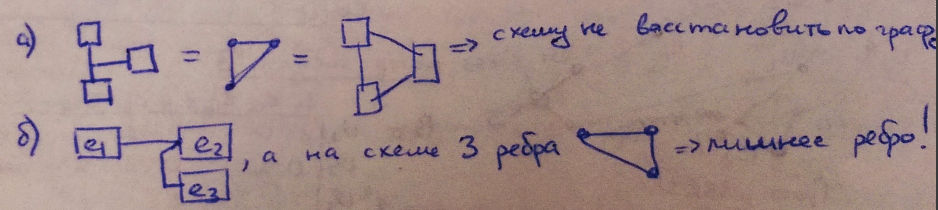
Минусы модели в невозможности восстановления схемы по такому графу: