Вопрос 5: Последовательные методы компановки узлов

Идея метода

В графе по определённому правилу определяется 1 или несколько вершин и назначаются в первый формируемый кусок. Затем, по определённым правилам в этот кусок добавляется ещё 1 или несколько вершин и этот процесс добавления повторяется до тех пор, пока кусок не будет сформирован. Факт формирования (конца) куска определяется заданными ограничениями. После этого вершины, вошедшие в него и инцидентные им рёбра исключают из исходного графа. К оставшимся частям графа применяется тот же алгоритм формирования куска.

Преимущества алгоритма:

• простота
• малые временные затраты на решение задач

Недостаток:

• относительно низкое качество решения задач

Пример последовательного алгоритма

Пусть имеется схема, заданная взвешенным графом схемы (ВГС).

Вес = кратность ребра.

Пример графа:

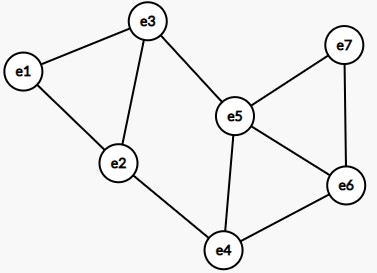
Матрица смежности для графа размерности n:

Задача: разбить граф на m кусков с числом вершин $L_1, L_2...L_m$.

Критерий: минимум числа межузловых соединений.

Куски формируют последовательно. Будем формировать первый кусок, содержащий $L_1$ вершин.

Алгоритм

ШАГ1: в исходном графе выбирается вершина с минимальной локальной степенью. (Минимальная локальная степень - число рёбер, примыкающих к вершине.) Выбранная вершина $e_i$ может быть названа ядром.

Далее выбираем следующую вершину с минимальной локальной степенью. Если таких вершин нет, то выбираем случайнм образом. Если вершин несколько. то выбирается вершина с большим числом кратных рёбер.

ШАГ2: выбранную вершину отправляем в подмножество $\Gamma e^*_j$ - группу вершин.

$e^*_j => \Gamma e^*_j$

ШАГ3: в подмножество $\Gamma e^*j$ добавляем все вершины смежные с добавленной на предыдущем шаге.

$\Gamma e_j = {e^*_j,e_j}$, где $e_j$ - смежна с $e^*_j$

ШАГ4: сравниваем мощность полученного подмножества с ограничением ($L_1$).

Возможны варианты: $|\Gamma e^*_j| = L1 =>$ переходим к 7 шагу. $|\Gamma e^*_j| > L1 =>$ переходим к 5 шагу. $|\Gamma e^*_j| < L1 =>$ переходим к 6 шагу.

ШАГ5: Из сформированного подмножества $\Gamma e^*_j$ удаляем вершину с min числом рёбер.Снова проверяем критерий (шаг4).

ШАГ6: добавить порцию вершин, среди вершин $e_j$ из $\Gamma e^*_j$ выбирается вершина, связанная с остальными вершинами данного подмножества наибольшим числом рёбер ($e^*_j$), т.е. смежную вершину, не принадлежащую $\Gamma e^*j$, но максимально связанную с $e_j$, принадлежащую $\Gamma e^*_j$. Добавляем её в $\Gamma e^*_j$ и проверяем критерий (Шаг4).

ШАГ7: (кусок сформирован)

Из исходного графа исключаются все вершины, вошедшие в кусок и инцидентные им рёбра. Оставляем часть необходимую для формирования следующего куска.

Алгоритм максимальной коньюнкции и минимальной дизъюнкции

Отличие: после выбора ядра назначаем по 1 вершине и повторяем цикл, связанный с выбором вершин.

Смысл: На каждом цикле куску назначается вершина с максимальным числом рёбер, но с минимальным числом рёбер, связанных с невыбранными элементами.

Последовательный алгоритм c последовательным формированием узлов

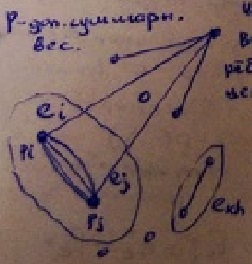
Пусть элементы равногабаритные (иначе вводят вес рёбер, чем больше размеры и площадь элементов, тем больше вес)

Выбирают пару вершин $e_i$ и $e_j$, связанную между собой максимальным числом рёбер. Объединяем их в 1 кусок, затем рассматриваются как единое целое, но объединяется при условии:

$r_ij -> max$

$p_i + p_j <= P$, где $P$ - суммарный вес

Пример: