Вопрос 20: Методы трассировки соединений внутри канала.

Одна из основных задач трассировка соединений внутри канала - выделение из множества соединений, отнесенных к каналу, минимального числа $h$ подмножеств отрезков, каждое из которых может быть назначено на одну магистраль канала.

Магистрали - осевые линии, по которым проходят трассы.

Если пропускная способность $\gamma$ канала задана, то должно быть выполнено условие $h \leq \gamma$.

Пусть дано множество отрезков $S = \{ M_1, M_2, ..., M_n \}$, отнесенных к этому каналу: $M_i = [ x^i_1, x^i_2 ], i = 1, 2, ..., n.$ Два отрезка не могут быть помещены на одну магистраль, если они пересекаются $M_i \cap M_j \neq \varnothing$

Граф интервалов

Графом интервалов $G(S)$ множества $S$ называюется граф, вершинами которого являются интервалы $M_i(i=1, 2, ..., n)$, а ребра соответствуют пересечению интервалов $M_i$ и $M_j$.

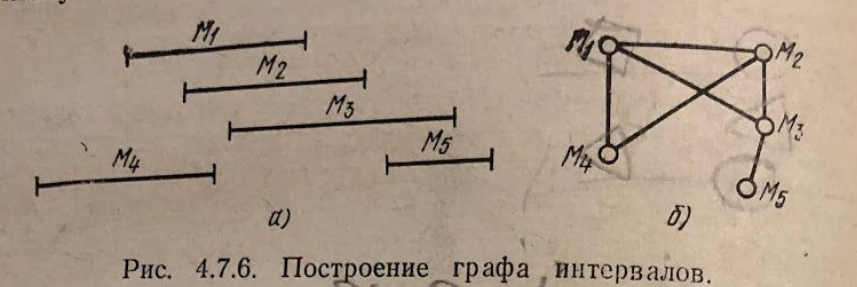
Таким образом задача оптимального использования магистралей формулируется, как задача получения минимальной раскраски вершин графа.

Алгоритм:

1. Упорядочить интервалы множества $S$ по левым концам: $M_1, M_2, ..., M_n$ ( $M_i < M_j$, если $x^i_1 < x^j_i$ )

2. После раскраски $k < n$ вершин $M_i (i=1, 2, .., k)$ вершину $M_{k+1}$ окрасить первой по порядку краской, которой не окрашены смежные с ней вершины из множества $\{ M_i, i=1, 2, .., k \}$

Граф горизонтальных ограничений (ГГО)

ГГО представляет собой неориентированный граф $G = (M, W)$, вершинами которого являются горизонтальные отрезки цепей $M_i$, а наличие дуги $w = (M_i, M_j)$ говорит о невозможности разместить элементы на одной магистрали $M_i \cap M_j \neq \varnothing$.

Граф вертикальных ограничений (ГВО)

Рассмотрим более общую задачу, когда минимизация числа горизонтальных связей осуществляется с учетом вертикальных связей между каналами.

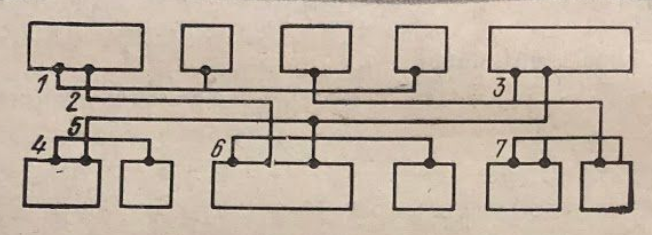
Будем считать, что горизонтальные отрезки соединений располагаются в слое металлизации, а вертикальные отрезки (подходы к выводам ячеек) в слое диффузии.

При распределении горизонтальных отрезков необходимо следить за тем, чтобы вертикальные отрезки, находящиеся в одном столбце, не перекрывались друг с другом. Зададим данные ограничения с помощью ориентированного графа $G = (M, U)$, вершинами которого являются горизонтальные отрезки цепей, а наличие дуги $u = (M_i, M_j)$ означает, что отрезок $M_i$ расположен на магистрали, находящейся над магистралью отрезка $M_j$.

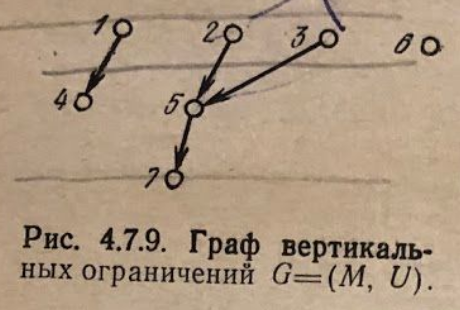
В случае, если ГВО содержит циклы, может потребоваться несколько горизонтальных отрезков.

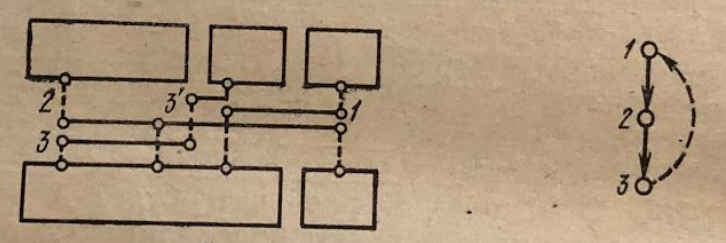
Таким образом задача состоит в минимизации числа используемых магистралей при соблюдении порядка расположения горизонтальных отрезков цепей.

Алгоритм:

1. Упорядочить множество горизонтальных отрезков $S = (M_1, M_2, ..., M_n)$ по левым концам.
2. Применить ранее описанный алгоритм раскраски графа интервалов $G(S)$ с одним дополнением: при назначении цвета для очередной вершины $M_{k+1}$ проверяется не только смежность ее с вершинами из множества $R_k = \{ M_i, i = 1, 2, ..., k \}$, но и отношение порядка в графе вертикальных ограничений $G = (M, U)$. Иными словами, пусть $l(M_i)$ - номер магистрали для отрезка $M_i$. Тогда:

$L_k = \{ M_i : M_i \in R_k, M_i \cap M_{k+1} = \varnothing \},$

$T_k = \{ M_i : M_i \in R_k, (M_i, M_{k+1}) \in U \in G(M,U) \}$

$l(M_{k+1}) = \min_{M_i \in R_k \setminus L_k} l(M_i) > \max_{M_i \in T_k} l(M_i)$

Решение проблемы перекрестков

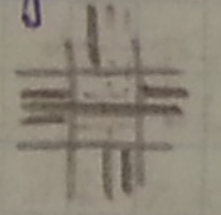
Участки, занятые перекрестком, не рассматриваются:

• Соединения, меняющие направление, доводятся до границы перекрестка.
• Соединения, не меняющие направления, проходят напрямую сквозь перекресток.
• Перекресток рассматривается отдельным алгоритмом (напр. волновым)