Вопрос 8: Последовательные методы размещения элементов

Рассмотрим размещение в фиксированные позиции

По определённому правилу определяется очередной размещаемый элемент, затем, по определённому правилу, для элемента выбирается позиция, и выбранный элемент закрепляется за за выбранной позицией окончательно. Если нет изначально установленных дискретных элементов, то алгоритм должен содержать особое правило для первого элемента и для позиции первого элемента.

Набор правил:

Правило выбора очередного размещаемого элемента (k-й шаг):

• $E_k$ – размещённые элементы;
• $\overline{E_k}$ – не размещённые элементы;
• $p_k$ – занятые позиции;
• $\overline{p_k}$ – незанятые позиции;
• $e_k$ – очередной размещаемый элемент;

1. Правило 1

В качестве очередного размещаемого элемента $e_k$ выбирается элемент из $\overline{E_k}$, для которого $c_k = r_{kj}$, где $e_j \in E_k \rightarrow max$

1. Правило 2

Из $\overline{E_k}$ выбирается $c_k = max \sum_{j}^{} r_{kj}$, $e_j \in E_k$. Если элементов несколько, смотрим, у кого меньше связей с не размещёнными элементами. Если сумма рёбер нескольких элементов одинакова, то считать для них $\alpha$ $\rightarrow$ символ связаности (ниже).

1. Правило 3

В качестве очередного $e_k$ выбирается такой элемент из $\overline{E_k}$, что $c_k = \sum_{j}^{} r_{kj} - \sum_{\alpha}^{} r_{k\alpha}$, где $e_j \in E_k, e_{\alpha} \in \overline{E_k}$

1. Правило 4

$c_k = \frac{\sum_{j}^{} r_{kj} }{\rho(e_k)}$, вес ребра: $\gamma = \frac{2}{\rho(\vartheta_i)}$

Правило выбора позиций

Критерий - $min \sum_{}^{}$ длины соединений. Определение начального значения критерия, по которому работаем.

Стоит рассматривать позиции, ближайшие к занятым.

1. В качестве позиции для очередного размещаемого элемента выбирается позиция $p_i^*$ из числа свободных, при установке в которую длина, т.е. критерий, стремится к минимуму.

$L = \sum_{j}^{} r_{kj} d_{p_i^j p_j}$, где $e_j \in E_k$, т.е. считаем приращение суммарной длины соединений

Пример: предположим, что есть некое подмножество элементов $E_k$ (несколько элементов) и есть $\overline{E_k}$.

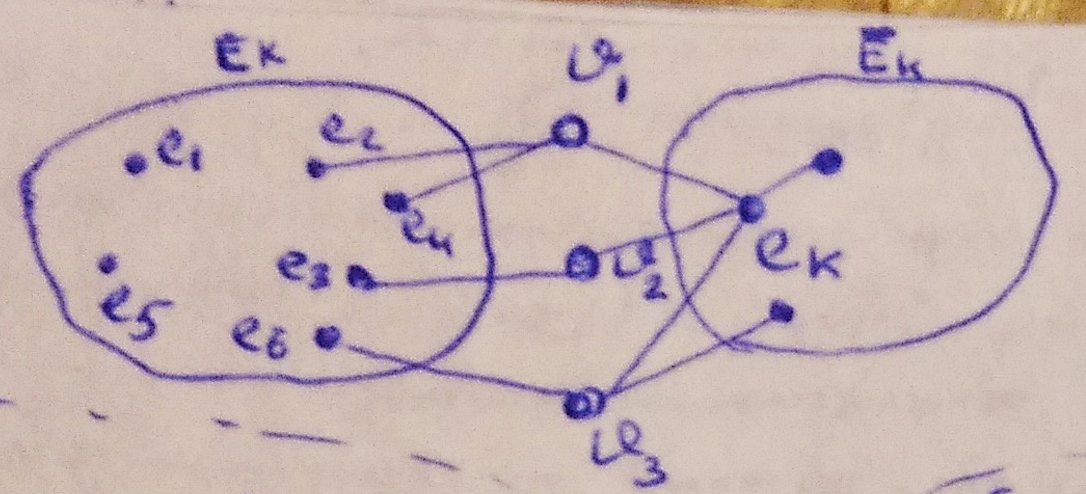
1. В качестве позиций очередного размещаемого элемента выбирается та позиция из числа свободных, для которой функционал $F = \sum_{s}^{} d_{i^*}^s, s \in I_{kj}, e_j \in E_k \rightarrow min$

$I_{kj}$ – номера цепей (подмножества), связывающие элемент $e_k$ с ранее размещёнными элементами схемы (суммирование идёт по всем цепям) $d_{i^*}^s$ – расстояние от рассматриваемой позиции $i$ до ближайшего ранее размещённого элемента в цепи с номером $s$:

$p' \Rightarrow d_{p'}^1 = 2; d_{p'}^2 = 2; d_{p'}^3 = 3 \Rightarrow F = 7$

$p'' \Rightarrow d_{p''}^1 = 3; d_{p''}^2 = 2; d_{p''}^3 = 1 \Rightarrow F = 6$

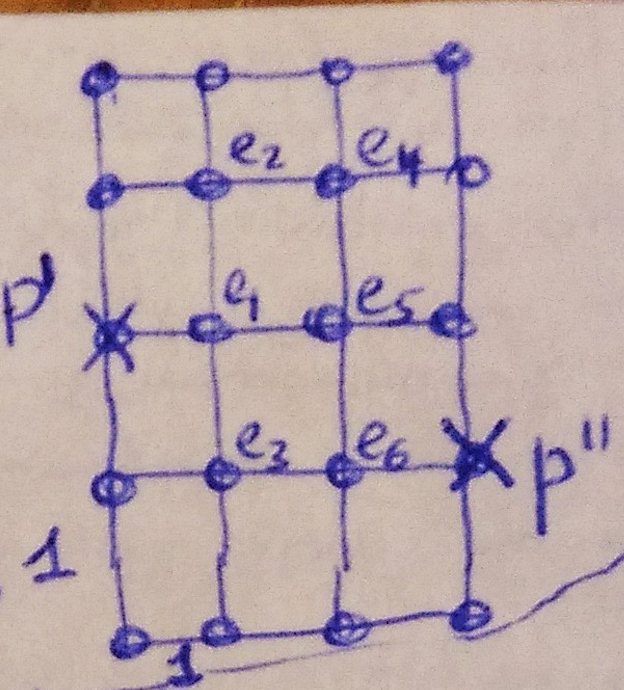
Следовательно, выбираем позицию 2. Алгоритм Прима – последовательный алгоритм.

1. Правило выбора очередного $e_k$ : в качестве позиции для $e_k$ выбираем такую позицию, в которой сумма полупериметра $F = \sum_{s}^{} \prod_{kj}^s \rightarrow min$

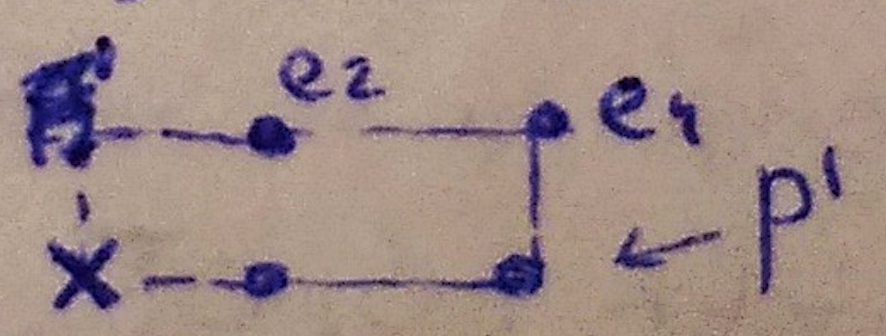
1. Для выбора позиций среди равноценных с точки зрения правил 1-3 можно воспользоваться следующим дополнительным правилом:

Выбирается позиция, лежащая ближе к "центру масс" – точке, имеющей координаты: $x_{cm} = \frac{ \sum_{j}^{} r_{kj} d_p(k) p(j) }{ \sum_{j}^{} r_{kj} }, y_{cm} = \frac{ \sum_{j}^{} r_{kj} d_p(k) p(j) }{ \sum_{j}^{} r_{kj} }$

Если имеем заранее размещённые элементы, то в качестве первого размещаемого элемента берём элемент с max локальной степенью, т.е. элемент, который инцидентен наибольшему числу элементов. Позиция для данного элемента выбирается из тех, у которых сумма расстояний от неё до всех остальных стремится к минимуму.