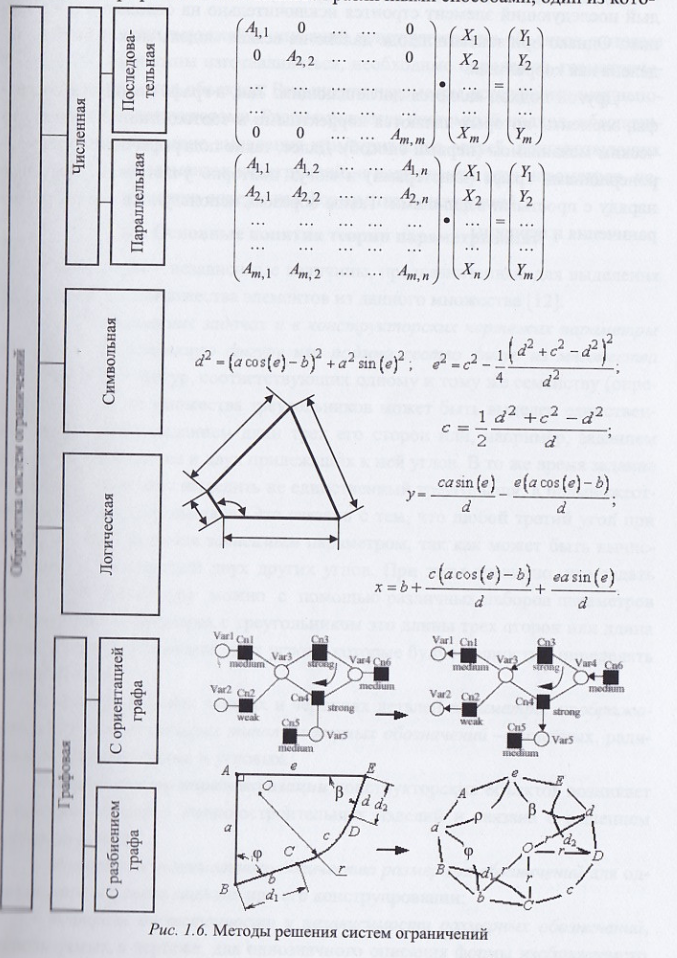
Вопрос 54: Полнота системы ограничений и методы разрешения системы ограничений, используемых в конструкторских САПР.

Полнота системы ограничений.

Система ограничений, применяемая к конкретной модели, также имеет определенное значение. Она может быть:

• неполной, неопределенные параметры могут принимать бесконечное число значений => при модификации модели может быть построенно бесконечное число вариантов модифицированного объекта;
• правильный выбор для формирование модели, однозначно соотв. исходному заданию параметров этой модели полной, система может построить единственный вариант модифицированного объекта, точно соотв. заданным конструктором значениями задающих параметров;
• избыточной, в описании модели объекта имеются лишнии, зависимые от других параметров ограничения. Их можно либо удалить из общего списка и построить единств. вариант модифицированного объекта, либо оставить в описании модели. В последнем случае нужно доп. размерных обочночения использовать как справочные, иначе модель будет неработоспособной как неправильно сформированная. То есть система не сможет осуществ. модификацию объекта и вывод соотв. изображения. Значения справочных размеров при модификации изображения могут противоречить управляющим и вводить в заблуждение конструктор, если не применять соотв. средства автомат. коррекции их значений при преобразовании.

Решение системы ограничений

Двумерное пространство

• Численные методы: перевод огранчений в форму алгебраических уравнений и решение ее итерационным численным методом (Ньютона-Котеса, Гауса, Крамера, ...)

  • Достоинства: возможность решения избыточных систем ограничений при условии взаимной непротиворечивости отдельных ограничений.
  • Недостаток: ирациональный метод может найти только единственное решение из множества вариантов. Сходимость зависит от начальной конфигурации модели.
  • Применение: к моделям, полученные в ходе мягкой или жесткой параметризации.

• Символьные методы: Система уравнений решается не численными методами, а в общем виде. Далее, при подстановке конкретных значений в выражения, полученные в ходе решения задачи, получают вариант конфигурации объекта.

  • Недостаток: система уравнений должна быть независима, иначе решение не будет найдено.
  • Применение: обработка жестких параметрических моделей.

• Логические методы: Решение системы ограничений применяются правила логического вывода.

  Состав примитивов объекта: точки, линии, векторы и треугольники.

  Допустимые отношения: расстояние между двумя точками, углы между линиями либо 2 угла треугольника.

  Примитивы + отношения = система предикатов, после чего применяются правила евклидовой геометрии построения.

  • Достоинства: избавление от необходимости решения больших систем уравнений.
  • Недостатки: своеобразность построения моделей, ограниченный состав примитивов, применимость только для решения сравнительно небольших задач.

• Графовые методы:

  • С ориентацией графа: один из ранних подходов решения системы ограничений для построения моделей объектов.

    1. Строится система уравнений.
    2. В уравнениях выделяются константы и переменные.
    3. Строится неориентированный граф, вершины которого соотв. сами уравнения, а также переменные и константы. Ребра указывают принадлежность констант и переменных к уравнениям.
    4. Выполняется задача ориентации графа, начиная с вершины-констант.

  • С разбиением графа: один из прогрессивных методов.

    Вершины графа соотв. приметивам модели, а ребра - отношения между элементами.

    1. Этап анализа: Определяется характер системы ограничений. Она должна быть полной (необходимое условие).
    2. Этап построения: Генерация модели в виде последовательного нахождения пространственного положения примитивов.

  • Анализ графа

    1. Хронологический механизм моделирования: каждый последующий элемент строится исключительно на основании предыдущих. Но не всякая модель может быть определенна как корректная.

    2. Поглащение: в графе находятся подграфы, элементы которых являются корректными в соотв. с хронологическим механизмом (Первый способ). Далее подграфы считаются макровершинами графа (кластерами) и могут быть повторно участвовать в анализе наряду с простыми вершинами. Таким образом, используются все ребра, ограничения и вершины.