Вопрос 2: Модели представления объектов в САПР. Трёхмерные модели.
Для хранения и отображения геометрической информации в САПР могут использоваться различные графические модели. В соответствии с используемой для представления моделей координатной системой выделяют плоские (2D) и пространственные (3D) модели объектов. Наиболее прогрессивными являются 3D-модели, позволяющие достаточно наглядно отобразить математический образ объекта, наделить его необходимыми физическими свойствами и отследить динамику поведения объекта в пространстве. С другой стороны, 2D-модели более соответствуют характеристикам имеющихся устройств ввода/вывода ЭВМ и формальным требованиям к оформлению результатов проектных работ в соответствие со стандартами ЕСКД.
С точки зрения состава любая графическая модель состоит из множества элементарных двухмерных или трёхмерных графических примитивов (компонентов) и/или библиотечных элементов (макросов), представляющих собой не изменяющиеся законченные образы, составленные из совокупности примитивов.
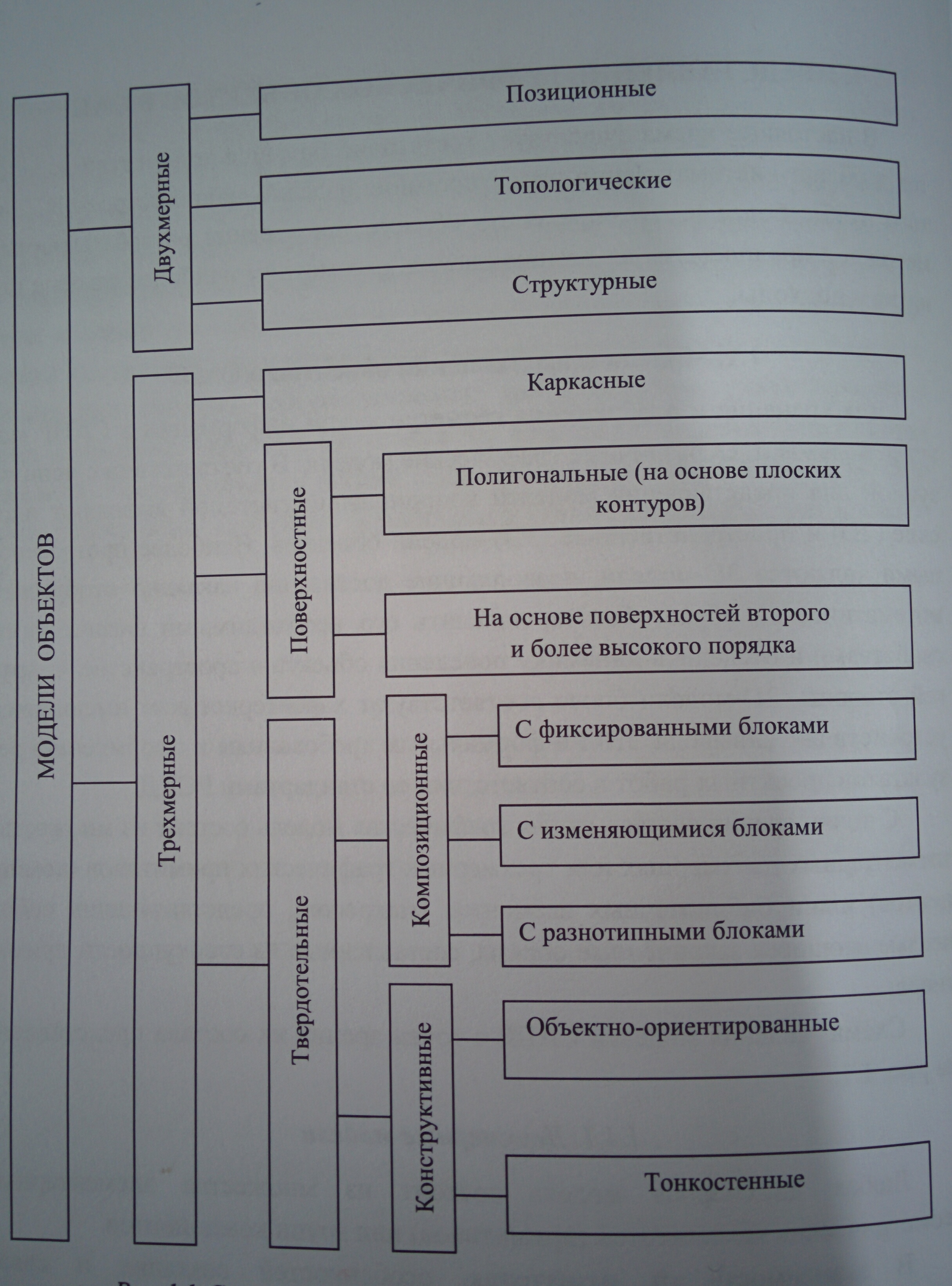
Трёхмерные модели.
Структурное деление 3D-моделей осуществляется в зависимости от характера геометрических или структурных элементов, составляющих основу модели. Здесь следует выделить проволочные (wire-frame) или каркасные (skeletal model) модели, полигональные (polygonal mesh), поверхностные (surface, nurbs), а также твердотельные (solid) модели.
Проволочные модели относятся к классу точечных моделей. Такое представление 3D-объектов было разработано ещё в начале 60-х годов и подразумевает пошаговое построение модели в терминах вершин и рёбер. Вершинам соответствуют пространственно-определённые точки, а соединяющим их рёбрам – прямые отрезки или кривые. Подобные модели имеют существенные недостатки, такие, как, например, возможность построения нереальных или неоднозначных моделей. Построение проволочных моделей весьма рутинно и неэффективно.
Поверхностные модели – дальнейшее развитие сеточного подхода к представлению 3D-объектов. Дополнительно к таблицам точек и рёбер, составляющих модель, вводится таблица граней, связывающих отдельные элементы сеточной модели. Грани – участки поверхностей – могут описываться множеством способов: аналитически, параметрически и т.д. Часто при задании поверхностей граней используются B-сплайны. Поверхностные модели достаточно широко распространены в современном САПР-моделировании, так как наиболее эффективно применимы для конструирования трёхмерных объектов произвольных нерегулярных форм.
Твердотельные модели представляют собой принципиально новый класс моделей. В отличие от ранее описанных контурных моделей подобные модели могут использоваться при решении широкого круга проектно-конструкторских подзадач, таких, как проверки пересечений, подсчёта объёмов и площади поверхности, анализа, например, механических напряжений в конструкции при использовании метода конечных элементов и при других исследованиях физических процессов в объектах. Это определяется тем, что твердотельные модели наиболее адекватно представляют реальные предметы. Можно выделить композиционные и конструктивные модели.
Представление 3D-объекта в композиционных моделях осуществляется его аппроксимацией малоразмерными 3D-примитивами, например, кубами, параллелепипедами, конусами и т.д.
Конструктивные твердотельные модели (CSG – Constructive Solid Geometry) на сегодняшний день наиболее эффективны. Формирование конструктивной 3D-модели осуществляется на основе булевых операций на базовыми объёмными примитивами, которые строятся тремя способами. При первом способе используется комбинирование простейших непроизводных трёхмерных графических примитивов с управляемыми параметрами, форма и размеры которых определяются непосредственно в процессе построения модели. Второй подход предполагает использование объёмных твердотельных базовых элементов (объёмных примитивов), создаваемых на основе формируемого эскиза сечения с использованием ряда специфических конструкторских операций. В третьем случае в одной системе используют оба указанных подхода при формировании твердотельной модели произвольного объёмного объекта.
Одним из важных понятий CSG является половинное деление пространства, при котором конструируемый 3D-элемент формируется отсечением от общего пространства его части соответствующей плоской поверхностью. При этом образуются «положительная» и «отрицательная» бесконечные стороны пространства. Логическая комбинация бесконечных полупространств даёт в конечном итоге требуемое конечное трёхмерное пространство-тело. Например, обыкновенный параллелепипед является комбинацией шести полупространств, определяемых взаимно-перпендикулярными плоскостями.
Простейшие примитивы, полученные в результате комбинаций полупространств, обеспечивают в дальнейшем построение конструктивной твердотельной модели на основании булевых операций над ними. Дополнительно к таким примитивам добавляются примитивы, полученные перемещением плоской грани вдоль определённой траектории (sweeps). К базовым CSG-примитивам можно отнести такие объекты, как параллелепипеды, конусы, цилиндры, сферы, торы и др. Операции, производимые над примитивами – объединение, пересечение, вычитание. Объект, полученный посредством операции над базовыми примитивами, также может использоваться в качестве операнда последующих булевых операций.