Вопрос 49: Контейнеры - хэш-таблицы
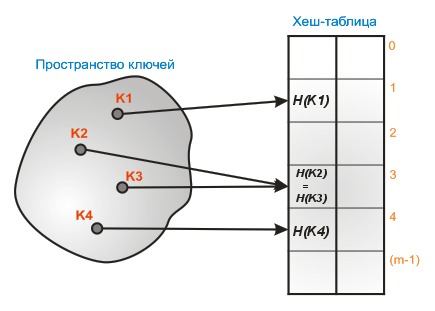
Хэш-таблица - обобщение способа хранения множества целых чисел (ключей) в форме вектора битов на случай, когда мощность универсума U очень велика по отношению к мощности множеств, с которыми нужно работать. Функция отображения преобразует значения ключей к интервалу [0, m-1], где m - размер хэш-таблицы, m << |U|. В хэш-таблице хранятся значения ключей и имеется возможность размещения в ней более одного ключа для каждого значения функции отображения (разрешать коллизии). Условия уменьшения возможности коллизий:
- Размер хэш-таблицы с запасом. Если размер таблицы превышает мощность хранимого множества более чем вдвое, вероятность коллизии становится меньше 0.5. Если размер множества заранее не известен, то выбирают начальный размер, а затем таблицу перестраивают с увеличением размера (обычно вдвое).
- Подобрать функцию отображения (хэш-функцию) такую, чтобы все ячейки таблицы были востребованы с равной вероятностью.
По способу разрешения коллизий различают хэш-таблицы двух типов:
- С открытой адресацией. Конфликтующие значения ключей размещаются в свободных ячейках таблицы.
- С цепочками переполнения. Каждая ячейка таблицы содержит указатель на список конфликтующих ключей.
В первой таблице все элементы хранятся непосредственно в хэш-таблице, без использования связанных списков. При переполнении таблицы применяется динамическое увеличение размера таблицы. Для разрешени коллизий применяются несколько подходов. Самый простой - метод линейного исследования: в случае коллизии проверяются все ячейки одна за другой, пока не найдётся пустая ячейка (при достижении конца таблицы, поиск продолжается с начала таблицы). Главная проблема - кластеризация (длинная последовательность занятых ячеек).
Во второй таблице, объединённые элементы, хэшированные в одну ячейку, формируют связный список. Процедура вставки в худшем случае выполнится за O(1). Время поиска зависит от длины списка, и в худшем случае равно O(n), при условии, что всё хэшируется в одну ячейку. Если функция распределит n ключей по m ячейкам равномерно, то в каждом списке будет содержаться порядка n/m ключей. Это число называется коэффициентом заполнения. В среднем случае все операции в такой таблице выполняются за время O(1).
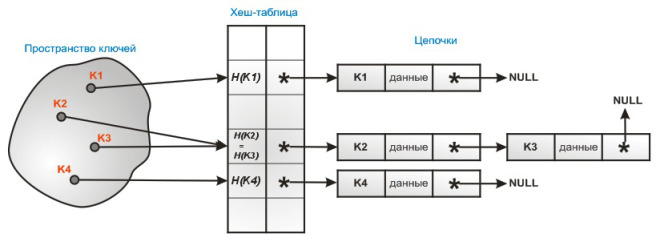
Таблица второго типа применяестя чаще, потому что для них не существует проблемы переполнения. При слишком большой мощности хранимого множества таблица работает как m списков. В хэш-таблице можно хранить и множество с повторениями: совпадающие значения ключей не создают никаких проблем, кроме коллизий, которые решаются обычным образом. Худший случай оценки времени: O(n) - для поиска и удаления элемента, O(n^2) - для двуместной операции над множествами. Если ключи - целые числа, то хорошие результаты можно получить с хэш-функцией вида: h(x) = (a * x + b) % m где m - таблицы, а a и b - простые числа. Обычно a выбирается близким по значению к m, а b - к 1. Так, при m = 100 можно взять a = 97, b = 11. Такой выбор обеспечивает равномерное использование всех ячеек в большинстве практичесикх случаев.