Вопрос 3: Дерево двоичного поиска как расширяемый список с сохранением упорядоченности

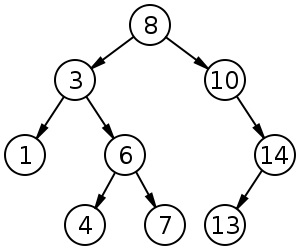
Дерево двоичного поиска (ДДП) - способ хранения множества в форме расширяемого упорядоченного списка с сохранением упорядоченности при вставке новых элементов без перемещения уже имеющихся.

ДДП - это дерево с нагруженными узлами, вес в любом узле которого больше любого веса в левом его поддереве и не больше любого веса в правом поддереве. Колличество шагов алгоритма поиска элемента множества в таком дереве не превышает его высоты, т.е. имеет сложность $O(log n)$. Такую же сложность имеют операции вставки нового элемента в дерево и удаления элемента.

ДДП можно получить из упорядоченной последовательности ключей, если двоичное дерево соответствующей мощности разместить внутренним (симметричным) способом, а затем заменить номера узлов соответствующими элементами последовательности. Если последовательность хранится в массиве, то построить ДДП можно методом деления пополам: поместить в корень дерева средний по порядку элемент, затем рекурсивно создать левое поддерево из первой половины последовательности, а правое - из второй.

Node* build(int a, int b, int* data) // Сборка ДДП из массива узлов data
{
    if (b <= a)
        return 0;

    int c = (a + b) / 2;
    Node* s = new Node(data[c]);

    s->left = build(a, c, data);
    s->right = build(c + 1, b, data);

    return s;
}

Недостаток ДДП - хорошо работает только в том случае, если оно сбалансированно, т.е. длины путей из корня в любой лист примерно одинаковы. Однако, при поэлементной вставке в дерево упорядоченной последовательности дерево вырождается, превращаясь в линейный список. Поиск, вставка и удаление в таком дереве будут выполняться не за логарифмическое время, а за линейное время. Вероятность вырождения весьма велика. Так, из 7 узлов можно образовать только одно полностью сбалансированное дерево, а полностью вырожденных - 64. Поэтому алгоритмы работы с ДДП часто дополняют автобалансировкой после вставки и удаления. Наиболее употребительны следующие схемы:

1. АВЛ - деревья. Разность высот поддеревьев любого узла дерева не превышает 1. Информация о разности высот хранится в узле и используется для его перестройки после вставки и удаления узла.
2. Красно-чёрные деревья. Узлы красятся в один из двух цветов - чёрный или красный. Если узел - красный, его сыновья - обязательно чёрные. Вставляемый узел - всегда красный. При появлении цепочки из двух красных узлов дерево перестраивается.
3. 2-3 - деревья. Данные хранятся в листьях, над которыми делается надстройка из управляющих узлов, каждый из которых может иметь 2 или 3 сына и содержит наибольшие значения ключей в левом и в средне поддеревьях, что необходимо для операции поиска. Если в результате вставки или удаления у управляющего узла оказывается 1 или 4 сына, дерево перестраивается.

ДДП малопригодны для хранения множеств с повторениями: дубликаты ключей искажают дерево, образуя в нём мёртвые зоны (группы неиспользуемых указателей). Этого можно исбежать если вместо дубликатов ключей хранить в каждом узле значение кратности (1 или больше). Если же дубликаты должны быть представлены явно, их можно хранить в узлах как цепочки переполнения, по аналогии с хэш-таблицей.

Временная сложность двуместной операции будет в среднем $O(n*log n)$. В худшем случае, при вырожденных деревьях, двуместная операция потребует $O(n^2)$ времени. Из ДДП легко получить упорядоченную последовательность ключей внутренним обходом. Применив такой обход к двум ДДП одновременно, можно обработать последовательности алгоритмов слияния. Результат в виде упорядоченной последовательности записывается в массив из которого затем делением пополам строится новое ДДП. Независимо от исходных данных результат будет получен за $O(n)$ и сбалансированный.