Вопрос 11: АВЛ-дерево: алгоритмы балансировки при вставке и удалении.

АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.

Балансировка

Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится <= 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.

Используются 4 типа вращений:

Тут h(X) - высота дерева X

1. Малое левое вращение:

   

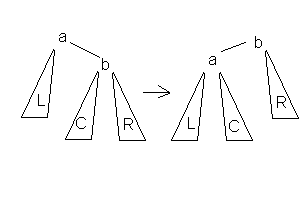
   Данное вращение используется тогда, когда (h(b) — h(L)) == 2 && h(С) <= h(R).

1. Большое левое вращение:

   

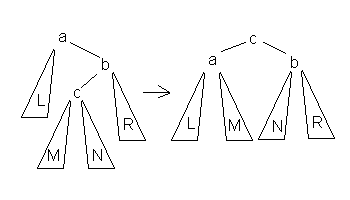
   Данное вращение используется тогда, когда высота (h(b) — h(L)) == 2 && h(c) > h(R).

1. Малое правое вращение:

   

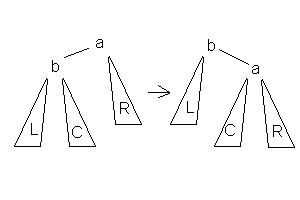
   Данное вращение используется тогда, когда высота (h(b) — h(R)) == 2 && h(C) <= h(L).

1. Большое правое вращение:

   

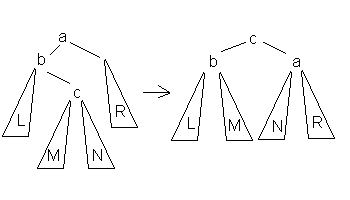
   Данное вращение используется тогда, когда (h(b) — h(R)) == 2 && h(c) > h(L).

В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться. Также можно заметить, что большое вращение это комбинация правого и левого малого вращения. Из-за условия балансированности высота дерева $O(log(N))$, где N- количество вершин, поэтому добавление элемента требует $O(log(N))$ операций.

Будем представлять узлы АВЛ-дерева следующей структурой:

struct node // структура для представления узлов дерева
{
    int key;
    unsigned char height;
    node* left;
    node* right;
    node(int k) {
        key = k;
        left = right = nullptr;
        height = 1;
    }
};

Поле key хранит ключ узла, поле height — высоту поддерева с корнем в данном узле, поля left и right — указатели на левое и правое поддеревья. Простой конструктор создает новый узел (высоты 1) с заданным ключом k.

Определим три вспомогательные функции, связанные с высотой. Первая является оберткой для поля height, она может работать и с нулевыми указателями (с пустыми деревьями):

unsigned char height(node* p)
{
    return p?p->height:0;
}

Вторая вычисляет balance factor заданного узла (и работает только с ненулевыми указателями):

int bfactor(node* p)
{
    return height(p->right)-height(p->left);
}

Третья функция восстанавливает корректное значение поля height заданного узла (при условии, что значения этого поля в правом и левом дочерних узлах являются корректными):

void fixheight(node* p)
{
    unsigned char hl = height(p->left);
    unsigned char hr = height(p->right);
    p->height = (hl>hr?hl:hr)+1;
}

Заметим, что все три функции являются нерекурсивными, т.е. время их работы есть величина $O(1)$.

Код, реализующий правый поворот, выглядит следующим образом (как обычно, каждая функция, изменяющая дерево, возвращает новый корень полученного дерева):

node* rotateright(node* p) // малый правый поворот вокруг p
{
    node* q = p->left;
    p->left = q->right;
    q->right = p;
    fixheight(p);
    fixheight(q);
    return q;
}

Левый поворот является симметричной копией правого:

node* rotateleft(node* q) // малый левый поворот вокруг q
{
    node* p = q->right;
    q->right = p->left;
    p->left = q;
    fixheight(q);
    fixheight(p);
    return p;
}

Код, выполняющий балансировку, сводится к проверке условий и выполнению поворотов:

node* balance(node* p) // балансировка узла p
{
    fixheight(p);
    if( bfactor(p)==2 )
    {
        if( bfactor(p->right) < 0 )
            p->right = rotateright(p->right);
        return rotateleft(p);
    }
    if( bfactor(p)==-2 )
    {
        if( bfactor(p->left) > 0  )
            p->left = rotateleft(p->left);
        return rotateright(p);
    }
    return p; // балансировка не нужна
}

Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.

Вставка нового ключа в АВЛ-дерево выполняется, по большому счету, так же, как это делается в простых деревьях поиска: спускаемся вниз по дереву, выбирая правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. Единственное отличие заключается в том, что при возвращении из рекурсии (т.е. после того, как ключ вставлен либо в правое, либо в левое поддерево, и это дерево сбалансировано) выполняется балансировка текущего узла.

node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
    if( !p ) return new node(k);
    if( k<p->key )
        p->left = insert(p->left,k);
    else
        p->right = insert(p->right,k);
    return balance(p);
}

Удаление ключа: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min.

При реализации возникает несколько нюансов. Прежде всего, если у найденный узел p не имеет правого поддерева, то по свойству АВЛ-дерева слева у этого узла может быть только один единственный дочерний узел (дерево высоты 1), либо узел p вообще лист. В обоих этих случаях надо просто удалить узел p и вернуть в качестве результата указатель на левый дочерний узел узла p.

Пусть теперь правое поддерево у p есть. Находим минимальный ключ в этом поддереве. По свойству двоичного дерева поиска этот ключ находится в конце левой ветки, начиная от корня дерева. Применяем рекурсивную функцию:

node* findmin(node* p) // поиск узла с минимальным ключом в дереве p 
{
    return p->left?findmin(p->left):p;
}

Еще одна служебная функция у нас будет заниматься удалением минимального элемента из заданного дерева. Опять же, по свойству АВЛ-дерева у минимального элемента справа либо подвешен единственный узел, либо там пусто. В обоих случаях надо просто вернуть указатель на правый узел и по пути назад (при возвращении из рекурсии) выполнить балансировку. Сам минимальный узел не удаляется, т.к. он нам еще пригодится.

node* removemin(node* p) // удаление узла с минимальным ключом из дерева p
{
    if( p->left==0 )
        return p->right;
    p->left = removemin(p->left);
    return balance(p);
}

Удаление ключа:

node* remove(node* p, int k) // удаление ключа k из дерева p
{
    if( !p ) return 0;
    if( k < p->key )
        p->left = remove(p->left,k);
    else if( k > p->key )
        p->right = remove(p->right,k);    

/*Как только ключ k найден, переходим к плану Б: 
запоминаем корни q и r левого и правого поддеревьев 
узла p; удаляем узел p; если правое поддерево пустое, 
то возвращаем указатель на левое поддерево; если правое 
поддерево не пустое, то находим там минимальный элемент 
min, потом его извлекаем оттуда, слева к min подвешиваем 
q, справа — то, что получилось из r, возвращаем min после 
его балансировки.*/

    else //  k == p->key 
    {
        node* q = p->left;
        node* r = p->right;
        delete p;
        if( !r ) return q;
        node* min = findmin(r);
        min->right = removemin(r);
        min->left = q;
        return balance(min);
    }

/*При выходе из рекурсии не забываем выполнить балансировку:*/

    return balance(p);
}

Очевидно, что операции вставки и удаления (а также более простая операция поиска) выполняются за время пропорциональное высоте дерева, т.к. в процессе выполнения этих операций производится спуск из корня к заданному узлу, и на каждом уровне выполняется некоторое фиксированное число действий. А в силу того, что АВЛ-дерево является сбалансированным, его высота зависит логарифмически от числа узлов. Таким образом, время выполнения всех трех базовых операций гарантированно логарифмически зависит от числа узлов дерева.