Вопросы 52: Алгоритм эволюции разума

Концепцию алгоритма эволюции разума (Mind Evolutionary Computation, MEC) предложил в 1998 г. Ченгай с соавторами. Алгоритм MEC моделирует некоторые аспекты поведения человека в обществе, а не работу человеческого мозга, как можно было бы предположить. В алгоритме MEC каждый индивид рассматривается как разумный агент, функционирующий в некоторой группе людей. При принятии решений он ощущает влияние как со стороны членов своей группы, так и со стороны членов других групп. Точнее говоря, чтобы достичь высокого положения в обществе, индивиду приходится учиться у наиболее успешных индивидов в своей группе. В то же время, для того чтобы группа, которой принадлежит данный индивид, становилась более успешной по сравнению с другими группами, этот индивид, как и все индивиды его группы, должны руководствоваться тем же самым принципом в межгрупповой конкуренции.

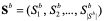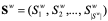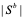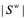Алгоритм MEC удобно интерпретировать как многопопуляционный алгоритм. Мультипопуляция алгоритма MEC состоит из лидирующих групп (superior groups) и отстающих групп (temporary groups) числом и соответственно. В оригинальном алгоритме MEC числа агентов в каждой из групп полагаются одинаковыми и равными .

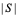Каждая из групп 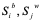имеет свою коммуникационную среду, которая названа авторами алгоритма локальной доской объявлений (local billboard). Обозначим эти доски 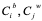соответственно. Кроме того, вся мультипопуляция 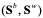имеет общую глобальную доску объявлений (global billboard) .

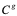Если далее в обозначениях групп и соответствующих локальных досок объявлений индексы 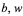опущены, то имеется в виду произвольная из этих групп и их досок объявлений. Полагаем, что речь идет о задаче условной максимизации в параллелепипеде .

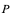Исходная версия алгоритма MEC, названная авторами простым алгоритмом эволюции разума (Simple MEC, SMEC), построена на основе операций инициализации групп, локальных состязаний (similar-taxis) и диссимиляции (dissimilation).

Операция инициализации групп создает группы 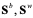из 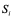агентов каждая и размещает их в области поиска. Рассмотрим схему операции на примере группы .

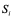• Генерируем случайный вектор 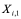, компоненты которого равномерно распределены в области поиска 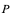. Отождествляем этот вектор с индивидом 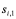группы ;
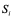• определяем начальные координаты остальных агентов данной группы 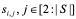, по формуле

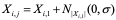(1)

т.е. размещаем случайным образом вокруг агента 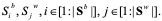(1) в соответствии с нормальным законом распределения.

Операция локальных состязаний реализует локальный поиск максимума фитнесс-функции каждой из групп Рассмотрим в качестве примера схему этой операции для группы :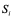

1) с доски объявлений 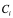берем информацию о текущем агенте-победителе группы 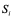(1) . Пусть это будет агент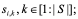

2) определяем новые координаты остальных агентов 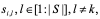(1) данной группы по правилу вида (1), т.е. размещаем случайным образом вокруг победителя в соответствии с нормальным законом распределения;

3) вычисляем новые счета (scores) агентов группы 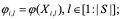(1)

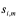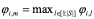4) определяем нового победителя группы (1) , т.е. агента данной группы, который имеет максимальный текущий счет: (1) ;

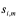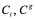5) заносим информацию о новом победителе группы (1) на доски объявлений (1).

Операция диссимиляции управляет глобальным поиском. Схема операции имеет следующий вид:

1) с глобальной доски объявлений 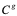считываем счета 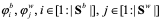всех групп (т.е. текущие счета победителей этих групп);

2) выполняем сравнение указанных счетов между собой. Если счет некоторой лидирующей группы 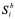меньше счета одной из отстающих групп 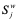, то последняя группа занимает место группы 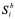во множестве лидирующих групп, а группа 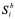– место группы 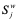среди отстающих групп. Если счет группы 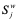ниже счетов всех отстающих групп, то удаляем группу 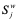из популяции;

3) с помощью операции инициализации вместо каждой из удаленных групп инициализируем новую группу.

В алгоритме SMEC операции локальных состязаний и диссимиляции итерационно повторяются до тех пор, пока имеет место увеличение максимального счета лидирующих групп. При прекращении роста этого счета решение задачи, соответствующее победителю лучшей из лидирующих групп, объявляется точкой глобального экстремума.